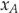: Anzahl Modell A
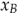: Anzahl Modell BAutohersteller, zwei Modelle A, B
| Modell | Montage | Endfertigung | Profit | Mindestzahl |
|---|---|---|---|---|
| A | 4h | 6h | 400 € | 20 |
| B | 6h | 3h | 300 € | 30 |
| Kapazität | 720h | 480h | max. |
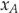: Anzahl Modell A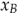: Anzahl Modell BZielfunktion: ![$f[x_A, x_b] = 400 x_A + 300 x_B$](temp-30265bf6.png "$f[x_A, x_b] = 400 x_A + 300 x_B$")
Restriktionen
![$g_1[x_A_, x_B] = 4x_A + 6x_B - 720$](temp-f4827939.png "$g_1[x_A_, x_B] = 4x_A + 6x_B - 720$")
![$g_2[x_A_, x_B] = 6x_A + 3x_B - 480$](temp-d2c32814.png "$g_2[x_A_, x_B] = 6x_A + 3x_B - 480$")
![$g_3[x_A_, x_B] = 20 - x_A$](temp-f411a50f.png "$g_3[x_A_, x_B] = 20 - x_A$")
![$g_4[x_A_, x_B] = 30 - x_B$](temp-1eaa08ae.png "$g_4[x_A_, x_B] = 30 - x_B$")
gesuchtes Optimum: ![$\max \{ f[x_A, x_B] \mid [x_A, x_B] \in M \}$](temp-1c7520d5.png "$\max \{ f[x_A, x_B] \mid [x_A, x_B] \in M \}$")
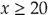
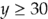
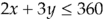
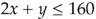
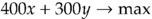
Grafisch: ![$S[30 / 100]$](temp-c0feb9ff.png "$S[30 / 100]$")
Zeigen Sie:
![\[K[x_o, r] = \{ x_0 \in \mathbb R_1 <x-x_0, x-x_0> \le r^2 \}\]](temp-fe0b19e9.png "\[K[x_o, r] = \{ x_0 \in \mathbb R_1 <x-x_0, x-x_0> \le r^2 \}\]")
ist konvex.
Hinweis: Zeigen Sie1, dass
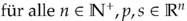gilt: ![$<p,p> \cdot <s,s> \ge [<p,s>]^2$](temp-e2f1baf3.png "$<p,p> \cdot <s,s> \ge [<p,s>]^2$")
.
1 Ungleichung von Cauchy